Số chính phương là gì? Cách nhận biết và ví dụ chi tiết
Bạn đang tìm hiểu về số chính phương là gì? Làm sao để nhận biết số chính phương? Mời bạn tham khảo bài viết đây để nắm rõ hơn những kiến thức về số chính phương thông qua các khái niệm và ví dụ chi tiết.

Những số chính phương đơn giản nhất (Nguồn Internet)
Số chính phương là gì?
Định nghĩa
Số chính phương là số bằng bình phương đúng của một số nguyên.
Hay hiểu đơn giản, số chính phương là một số tự nhiên có căn bậc hai cũng là một số tự nhiên. Số chính phương về bản chất là bình phương của một số tự nhiên nào đó. Số chính phương là diện tích của một hình vuông với cạnh là số nguyên kia.
Với số nguyên bao gồm các số nguyên dương, nguyên âm và số 0.
Một số chính phương được gọi là số chính phương chẵn nếu như nó là bình phương của một số chẵn, ngược lại. Một số chính phương được gọi là số chính phương lẻ nếu như nó là bình phương của một số lẻ.
Tính chất
- Số chính phương chỉ có chữ số tận cùng là 0,1,4,5,6,9, nếu các số tận cùng là 2,3,7,8 thì không phải là số chính phương.
- Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
- Số chính phương chỉ có thể có 1 trong 2 dạng: 4n hoặc 4n + 1, không có số chính phương nào có dang 4n + 2 hoặc 4n + 3 (với n € N).
- Số chính phương chỉ có thể có 1 trong 2 dạng: 3n hoặc 3n + 1, không có số chính phương nào có dang 3n + 2 (với n € N).
- Số chính phương có chữ số tận cùng là 1 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
- Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
- Số chính phương tận cùng bằng 4 thì chữ số hàng chục là chữ số chẵn.
- Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
- Số chính phương chia hết cho 2 thì chia hết cho 4.
- Số chính phương chia hết cho 3 thì chia hết cho 9.
- Số chính phương chia hết cho 5 thì chia hết cho 25.
- Số chính phương chia hết cho 8 thì chia hết cho 16.
- Số chính phương chia cho 3 không bao giờ có số dư là 2; chia cho 4 không bao giờ dư 2 hoặc 3; số chính phương lẻ khi chia 8 luôn dư 1.
Ví dụ:
9(3)2; 36 (6)2; là số chính phương.
Công thức để tính hiệu của hai số chính phương:
a2 – b2 = (a+b)(a-b).
Ví dụ:
62 – 32 = (6+3)(6-3) = 9.3 = 27.
Số ước nguyên dương của số chính phương là một số lẻ.
Số chính phương chia hết cho số nguyên tố p thì chia hết cho p2.
Ví dụ:
Số chính phương 36 (62) chia hết cho 2 => 36 chia hết cho 4 (22)
Số chính phương 144 (122) chia hết cho 3 (144:3=48) => 144 chia hết cho 9 (144:9=16)
Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1 = 1, 4 = 1 + 3, 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7, 25 = 1 + 3 + 5 + 7 + 9, …v.v
Ví dụ số chính phương
Các chuyên đề toán ở trung học đã có rất nhiều dạng bài tập về số chính phương. Dựa theo khái niệm và tính chất phía trên, ta có một số ví dụ về số chính phương như sau:
Các số 4, 9, 16, 25, 36, 49, 64, 81, 144, 225, 576 đều là số chính phương.
- 4= 22 là một số chính phương chẵn
- 9= 32 là một số chính phương lẻ
- 16= 42 là một số chính phương chẵn
- 25 = 52 là một số chính phương lẻ
- 36= 62 là một số chính phương chẵn
- 225 = 152 là một số chính phương lẻ
- 289 = 172 là một số chính phương lẻ
- 576 = 242 là một số chính phương chẵn
- 1.000.000= 1.0002 là một số chính phương chẵn
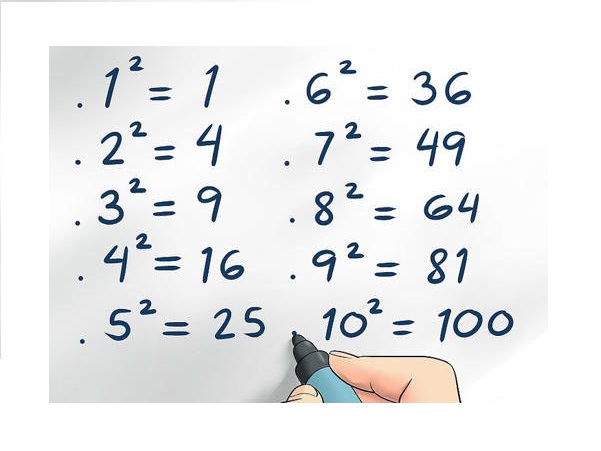
Số chính phương ứng dụng nhiều trong đời sống (Nguồn Internet)
Một số bài toán mẫu
Bài tập 1: Chứng minh một số không phải là số chính phương
Ví dụ 1: Chứng minh số n = 20042 + 20032 + 20022 – 20012 không phải là số chính phương.
Lời giải: Ta thấy chữ số tận cùng của các số 20042, 20032, 20022, 20012 lần lượt là 6,9,4,1. Do đó số n có chữ số tận cùng là 8 nên n không phải là số chính phương.
Ví dụ 2: Chứng minh 1234567890 không phải là số chính phương.
Lời giải: Ta thấy số 1234567890 chia hết cho 5 vì chữ số tận cùng là 0 nhưng lại không chia hết cho 25 vì hai chữ số tận cùng là 90. Vì vậy, số 1234567890 không phải là số chính phương.
Bài tập 2: Chứng minh một số là số chính phương
Chứng minh: Với mọi số tự nhiên n thì an = n(n+1)(n+2)(n+3) + 1 là số chính phương.
Lời giải:
Ta có:
an = n(n+1)(n+2)(n+3) + 1
= (n2 + 3n)(n2 + 3n + 2) +1
= (n2 + 3n)2+ 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
Với n là số tự nhiên thì (n2 + 3n + 1)2 cũng là số tự nhiên, vì vậy, an là số chính phương.

Số chính phương trong chương trình Toán học lớp 6 (Nguồn Internet)
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức có ích về số chính phương giúp cho công việc học tập và nghiên cứu của bạn thêm thuận lợi.
Tìm hiểu những thông tin chi tiết về phương trình mặt cầu: Toán học lớp 12 là nền tảng quan trọng nhất để các em học sinh có thể bổ sung kiến thức cho kì thi đại học sắp tới. Môn toán được chia thành 2 phần chính là đại số và hình học không gian. Công thức tính thể tích hình cầu và cách giải toán thể tích hình cầu đầy đủ nhất: Hình cầu là dạng hình học bắt gặp rất nhiều trong đời sống hàng ngày thông qua những vật dụng xung quanh chúng ta như quả bóng, quả địa cầu.
- Share CrocoBlock key trọn đời Download Crocoblock Free
- Cung cấp tài khoản nghe nhạc đỉnh cao Tidal Hifi – chất lượng âm thanh Master cho anh em mê nhạc.
- Cách bật tính năng ghi âm cuộc gọi tự động trên Android | Công Nghệ 4.0 | PLO
- Máy Làm Sữa Hạt Medion MD 19725 – Nhập Khẩu Đức | Giadungducsaigon
- Top 7 dịch vụ xem phim bản quyền tại nhà trong mùa Covid
- Cách khắc phục lỗi IDM không bắt link nhanh nhất | friend.com.vn
- Lỗi Protected View trong Excel 2010 và cách khác phục lỗi
Bài viết cùng chủ đề:
-
Cách giới hạn băng thông wifi trên router Tplink Totolink Tenda
-
Sự Thật Kinh Sợ Về Chiếc Vòng Ximen
-
"Kích hoạt nhanh tay – Mê say nhận quà" cùng ứng dụng Agribank E-Mobile Banking
-
Nên sử dụng bản Windows 10 nào? Home/Pro/Enter hay Edu
-
Cách gõ tiếng Việt trong ProShow Producer – Download.vn
-
Phân biệt các loại vạch kẻ đường và ý nghĩa của chúng để tránh bị phạt oan | anycar.vn
-
Câu điều kiện trong câu tường thuật
-
Gỡ bỏ các ứng dụng tự khởi động cùng Windows 7
-
Cách xem, xóa lịch sử duyệt web trên Google Chrome đơn giản
-
PCI Driver là gì? Update driver PCI Simple Communications Controller n
-
Sửa lỗi cách chữ trong Word cho mọi phiên bản 100% thành công…
-
Cách reset modem wifi TP link, thiết lập lại modem TP Link
-
Thao tác với vùng chọn trong Photoshop căn bản
-
Hình nền Hot Girl cho điện thoại đẹp nhất
-
Cách nhận dạng đồ thị hàm số mũ và logarit, bậc nhất, bậc 2, 3, 4
-
Chơi game kiếm tiền thật trên mạng uy tín 2021 – Nghialagi.org



